����15�N10��23���i�j��5�Z��
�j�q13���@���q14���@�v27��
���Ǝҁ@�����@�F�l
| TOP�y�[�W�� | �y�[�W�̍Ō�� |
�����̂����Z�Ƃ��Z���l���悤�i�����̂��Z�j
�@�{�w���̎����́A���܂��܂Ȋ����ɑ��Ĉӗ~�I�Ɏ��g�݁A���M�������Ă�肫�邱�Ƃ��ł���q�ǂ������ł���B�ۑ�����̊w�K�`�Ԃɂ�����Ă��āA�����̗͂ʼnۑ���������邱�Ƃ��y���ނ��Ƃ��ł���悤�ɂȂ��Ă��Ă���B2�w���͂��߂ɍs�����w�K�Ɋւ��钲���ł́A�N���X��3�����̎q�ǂ��������A�u���Z�v�ɑ��ċ��ӎ��������Ă��邱�Ƃ��킩�����B�����ŁA���ۂɂǂ̒��x���Ȃ̂��������Ƃ���A���Z���̂��̂����Ȃ̂ł͂Ȃ��A���܂���o������A����̈ʈȉ��̐����l�̌ܓ������肷��ȂǁA�ӂ��̂��Z�ɔ�ׂĎ菇����������̂���肾�Ƃ������Ƃ��킩�����B����́A����܂ł̐����̒��ŁA�u�v�Z�̈Ӗ������v�����u�v�Z�̕��@�����v��D�悷��悤�ȍl�������蒅���Ă��邱�Ƃ������ł��낤�ƍl������B�菇�⌅�������Ȃ�A�������킩��Ȃ��Ȃ��Ă����ꍇ�A�v�Z�̈Ӗ��𗝉����Ă���A������肪����ɖ����������Ƃ��\�ł���B�������A���Ղȕ��@�����ɗ����āA�Ӗ����������낻���ɂ��Ă������߂ɁA������Ƃł��܂����Ă��܂��Ɛ������o�����Ƃ��ł��Ȃ��Ȃ��Ă��܂��̂ł͂Ȃ����ƍl����̂ł���B�q�ǂ��������Ӗ��𗝉��ł���w�����@���H�v����K�v������ƍl���Ă���B
�@�{�P���ň��������Ə����̂����Z���Z�́A����܂łɊw�K���Ă��邩���Z���Z�̊w�K�������ɂ܂ōL������̂ł���B�����̊܂܂��v�Z�i�����~�����A�����������j�ɂ��ẮA���ł�1�w���Ɋw�K���Ă���B����ɐςݏd�˂Ă����`�ŁA�����Ə����̂����Z���Z�̊w�K���s���̂��{���ނł���B
�@�{���̊w�K�ł́A�������ł�����Ƃ��ɏ����폜�������傫���Ȃ邱�Ƃ��w�K����B�����ł��ꍇ�́A���͔폜�����傫���Ȃ邱�Ƃ͂Ȃ��B���̂��Ƃ́A�q�ǂ��������o����悭�킩���Ă��邱�Ƃł���B���������̋��ނł́A�����K�������폜����菬�����Ȃ�Ƃ͌���Ȃ����Ƃ��w�K���A�����ɑ���C���[�W�����������āA�u�������낢�v�u�s�v�c���v�Ƃ����C�����������o�����Ƃ��ł�����̂ƍl���Ă���B
�@�܂��{���ނł́A���ʊW�𗘗p���Ė����������ƂɂȂ��Ă���B����́A6�N���Ŋw�K����u�P�ʂ�����ʁv�̊w�K�ɂȂ����ȕ����ł����邽�߁A�m���Ȓ蒅��}���Ă��������ƍl���Ă���B
�@����̏����̂����Z���Z�̊w�K��i�߂�ɂ������āA2�̂��Ƃɏd�_��u���Ďw�������邱�Ƃɂ����B��ڂ́A�����\���I�ɂƂ炦�A�^����ꂽ�����Ƌ��߂Ȃ���Ȃ�Ȃ����Ƃm�ɂ��Ă�����Ɏ�肩����Ƃ������Ƃł���B����́A���͖�肩�當�ӂ�ǂ݂Ƃ�A�����̗͂Ŗ����������Ƃ����Ȏ����������������߂ł���B������́A���̐��̊W�����o�I�ɂ킩��₷������Ƃ������Ƃł���B�����́A�����̎v�������`�i�G��}�j�ɕ\���������s���A�q�ǂ��������ǂ̂悤�Ȃ��̂�`�����ώ@���Ă݂��B����ƁA���̏����Ƃ͊W�̂Ȃ�����ʂ�\���Ă݂���A���̊W��\���͂��̐}���A�����I�ɂ��������Ȑ}�ɂȂ��Ă�����Ƃ������X��������ꂽ�B�����ŁA�������}��{���}�Ȃǂ��g�������ʊW�̕\�������J��Ԃ��w�K�����Ď����̗͂ŕ`����悤�Ɏw�������B
�@�܂��A�P����ʂ��ē����悤�Ȍ`�̃��[�N�V�[�g��p�ӂ��A�w�K�`�Ԃ̃p�^�[������}�����B����ɂ���āA�q�ǂ������͊w�K�̗���ɑ��錩�ʂ������Ă�悤�ɂȂ�A���͉������X���[�Y�ɍs����悤�ɂȂ��Ă����B�܂��A���K������U��Ԃ�Ȃ���w�K��i�߂邱�Ƃ��e�ՂɂȂ�A�V���ȉۑ�ɑ��Ă��A�O���܂ł̊w�K��U��Ԃ�悢���Ƃ��o���I�ɗ������邱�Ƃ��ł���悤�ɂȂ��Ă��Ă���B
�@�{���̊w�K�ł́A�����ɉ����ăq���g�J�[�h���ƃJ�[�h�̊��p���l���Ă���B����́A���܂ł̊w�K�𗊂�ɁA�����̗͂ŗ������ł��Ȃ��q�ւ̎x���Ɛ��̊W��\���������}�������̂Ɏ��Ԃ�������q�ւ̎x���̂��߂ɗp���邱�Ƃɂ������̂ł���B����ɁA�����ł��Ă��܂��q�ɑ��ẮA�ʂ̖���p�ӂ��A�ۑ�ɑ��闝��������ɐ[�߂Ă��������ƍl���Ă���B
���搔�������̏ꍇ�̏�@��A�����������̏ꍇ�̏��@�̈Ӗ��Ƃ��̌v�Z�̂������ɂ��ė������A�����p����\�͂�L���B�܂��A�v�Z�@���͐��͈͂������̏ꍇ�ł����藧���Ƃ𗝉�����B
| �k�S�E�ӗ~�E�ԓx�l | ���搔�⏜���������̏ꍇ�ł��A���K�̐����̐��ʊW�Ȃǂ����Ƃɂ��āA��@�⏜�@�̎��ɕ\�����Ƃ���B |
| �k���w�I�ȍl�����l | �������̏�@�A���@�Ɗ֘A�Â��āA�搔�������̏�@�A�����������̏��@�̌v�Z�̂��������l����B |
| �k�\���E�����l | ���搔�������̏�@�A�����������̏��@�̌v�Z�����邱�Ƃ��ł���B |
| �k�m���E�����l | ���搔�������̏�@�A�����������̏��@�̈Ӗ��₻�̌v�Z�̂������𗝉�����B |
| ���P�� | ���� | �w�K���e | |
| 1.�����̂����Z | 8 | 2 | �E80�~2.7�̌v�Z�̂��������l���� �E80�~2.7�̌v�Z�̂��������܂Ƃ߂� |
| 1 | �E3.8�~2.6�̌v�Z�̂��������l���� �E�����ǂ�����������M�Z�̂��������܂Ƃ߂� |
||
| 1 | �E4.2�~7.5�A0.4�~2.3�̕M�Z�̂��������l���� | ||
| 1 | �E80�~1.8��80�~0.8�̌v�Z�����āA�ςƔ�搔�̑傫�����ׂ� �E��������������Ɛς���搔��菬�����Ȃ邱�Ƃ��܂Ƃ߂� |
||
| 1 | �E�c2.3cm�A��3.6cm�̒����`�̖ʐς̋��ߕ����l���� | ||
| 1 | �E�����A�����A���z�̖@���̎��ɏ����Ă͂߂āA�������藧�����ׂ� | ||
| 1 | �E�u���K�v������ | ||
| 2.�����̂��Z | 8 | 2 | �E200��2.5�̌v�Z�̂��������l���� �E200��2.5�̌v�Z�̂��������܂Ƃ߂� |
| 1 | �E8.5��2.5�̌v�Z�̂��������l���� �E�����������̕M�Z�̂��������܂Ƃ߂� |
||
| 1 | �E2.8��3.5�A1.8��2.4�Ȃǂ̕M�Z�̂��������l���� | ||
| 1 �{�� |
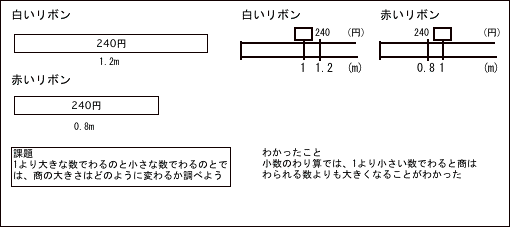
�E240��1.2��240��0.8�̌v�Z�����āA���Ɣ폜���̑傫�����ׂ� �E�������ł��Ə����폜�����傫���Ȃ邱�Ƃ��܂Ƃ߂� |
||
| 1 | �E2.5��0.7�ɂ����邠�܂���l���� �E�����̏��@�ɂ����邠�܂�̏����_�����ʒu�ɂ��Ă܂Ƃ߂� |
||
| 1 | �E�ʐ�7.2�F�̒����`�̉Ԃ���ŁA����2.9m�������ꍇ�̏c�̒��������߂� | ||
| 1 | �E�u���K�v������ | ||
| 3.�����{�Ƃ����Z�E���Z | 3 | 1 | �E3.6km�A1.8km�́A2.4km�̉��{�������߂���@���l���� �E��r�ʁA��ʂ������̏ꍇ�ł��{�����߂�ɂ́A���@���g�����Ƃ��܂Ƃ߂� |
| 1 | �E5m��3.5�{�A0.6�{�̒����̋��ߕ����l���� �E�����{�̂Ƃ�����r�ʂ͊�ʂ̉��{�ŋ��߂��邱�Ƃ��܂Ƃ߂� |
||
| 1 | 63kg����ʂ�1.8�{�ɂ�����Ƃ��́A��ʂ̋��ߕ����l���� | ||
| �܂Ƃ� | 1 | 1 | �u�������߁v������ |
�E�������i1��菬�������j�ł��ƁA���͔폜�����傫���Ȃ邱�Ƃ𗝉�����
| �O���̊w�K | �E2.8��3.5�A1.8��2.4�Ȃǂ̕M�Z�̂��������l���� | |||||
| �w�K���� | �w����̗��ӓ_ | �����ƕ]�� | ���� | |||
| 1.��ӂ��Ƃ炦�ė������� ���킩���Ă��邱�Ƃɐ��������܂��傤 �����߂Ȃ���Ȃ�Ȃ����Ƃɔg���������܂��傤 ���\�z�����Ă��玮�𗧂Ă܂��傤 ���Z���̂ɒl�i������������Ԃ̕������� �����߂Ă݂Ȃ���킩��Ȃ� |
�y���z �������{���́A1.2m��240�~�A�Ԃ����{���́A0.8m��240�~�ł��B1m�̂˂���́A���ꂼ�ꂢ����ɂȂ�܂����B �����[�N�V�[�g��z�z���A�����悭��Ƃ��ł���悤�ɂ��� ���������{���ƐԂ����{���̂��ꂼ��̒l�i�����߂Ȃ���Ȃ�Ȃ����Ƃ���������i2��������K�v������j ���ǂ��炪�������\�z�������Ă��痧�������� �E���c240��1.2�A�ԁc240��0.8 �������ɂƂ܂ǂ��Ă���q�ɂ́A�����ł�����ꍇ�̗����̕��@���v���o������ |
�E���[�N�V�[�g �E�������{���̐} �E�Ԃ����{���̐} �E�q���g�J�[�h ����ӂ𗝉����A�\�z�𗧂ĂĂ��痧�����邱�Ƃ��ł���i�ώ@�E���[�N�V�[�g�j |
10 | |||
��1m�̒l�i�́A���ꂼ�ꂢ����ɂȂ�܂��� ������鐔�������̕����傫���Ȃ����̂́A�ǂ���̃��{���ł��� ���Ԃ����{�����A����鐔�������̕����傫���Ȃ��� 3.����鐔�Ə��̑傫���̊W�ׂ� �����ꂼ��̐������}�����Ȃ���A��鐔�Ə��̑傫���̊W�ׂ܂��傤 ��1��菬�������ł��Ɠ���������鐔���傫���Ȃ� ������ē������傫���Ȃ�Ȃ�ĕs�v�c�� �����ׂ����ʂ\���悤 ��1���傫�����ł��ƁA���͂���鐔�����������Ȃ�A1��菬�������ł��ƁA���͂���鐔���傫���Ȃ��� 4.�������ł�����Ƃ��̏��Ɣ폜���̊W���܂Ƃ߂� ��1��菬�������ł�����Ƃ��A���͂ǂ��Ȃ邩�A���[�N�V�[�g�ɂ킩�������Ƃ������܂��傤 ��1��菬�������ł��ƁA��������鐔���傫���Ȃ邱�Ƃ��킩���� �����������Ƃ\���܂��傤 |
�����[�N�V�[�g�ɐ��̊W��\���}��`�����Đ��̊W���l�������� ����ƂɂƂ܂ǂ��q�ɂ́A��ƃJ�[�h��n���ăX���[�Y�ɍ�Ƃ��ł���悤�Ɏx������ ���Ԃ����{�����A����鐔���������傫���Ȃ��Ă��邱�ƂɋC�Â����� �������̂��Z�̂��������蒅�Ȏq�ɂ́A�������킩��悤�Ɏx������ ���������}����A1���傫�Ȑ��ł́A�����i�������Ȃ���j��1������A1��菬���������ł́A�E���i�傫���Ȃ���j��1�����邱�Ƃɒ��ڂ����� �����͂łł��Ȃ��q�ɂ́A�ʂɎx�����s�� �������ɏI����Ă��܂����q�ɁA�m�F�v�����g��z�z���A1.2��0.8�ȊO�̐��ł���Ă��̊W���m���߂����� ����\�҂ɔ��\�{�[�h���킽���āA���ׂ����Ƃ��������� �����\�{�[�h���g���āA�݂�Ȃɂ킩��₷�����\������ ���{���̊w�K�ɂ��āA�e���̌��t�ł܂Ƃ߂�悤�ɂ����� �����Ԏw���Ŕ��\�҂����炩���ߌ��߂Ă��� |
�E�ۑ� �E��ƃJ�[�h ���}��p���āA���Ƃ���鐔�̊W���l���悤�Ƃ���i�ώ@�E���[�N�V�[�g�j���}���肪����ɁA��鐔�Ɗ֘A�Â��Ă���鐔�Ə��̑召�W�ɂ��čl���Ă���i�ώ@�j �E�m�F�v�����g�E���\�{�[�h ��1��菬�������ł��ƁA��������鐔�����傫���Ȃ邱�Ƃ��킩��i�����E���[�N�V�[�g�j |
13 10 5 |
|||
| 5.�K�������������� �����[�N�V�[�g�̗��K�������܂��傤 ���������m�F���܂��傤 |
�����K���Ɏ��g�܂��� �����͂łł��Ȃ��q�ɂ́A�ʂɎx�����s�� |
���������ł��v�Z�����邱�Ƃ��ł���i�ώ@�E���[�N�V�[�g�j | 7 | |||
| �����̊w�K | �E2.5��0.7�ɂ����邠�܂���l���� �E�����̏��@�ɂ����邠�܂�̏����_�����ʒu�ɂ��Ă܂Ƃ߂� |
|||||
| TOP�y�[�W�� | �y�[�W�̍ŏ��� |