 |
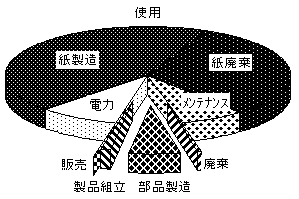
| 図1 複写機のCO2排出量割合(改訂前) |
科学技術庁、平成10年度環境基本計画推進調査費LCA応用施策に関する検討調査「物質・材料の研究開発および選択におけるLCAの導入に関する調査」報告書、19〜25(1999)
1.4 日本事務機械工業会における感度分析、誤差分析の取組について
1.4.1 はじめに
日本事務機械工業会では、約3年間を費やして複写機のLCAに関する検討をしてきた。昨年春に、これらの結果を報告書 [1] にまとめ、さらに結果の信頼性について感度分析 [2][3]や誤差分析を使って検討を続けている。本章では、複写機のLCAの検討結果を簡単に紹介し、次に複写機LCAへの感度分析や誤差分析の適用事例を紹介する。
1.4.2 複写機LCA
複写機のLCAは、「会員企業が複写機のLCAを実施するための算出モデルを提供する」ことなどを目的として実施した。複写機は、1996年に国内で製造販売されている30枚アナログ普通紙複写機の平均的な仮想機種(最大用紙サイズ:A3)を想定し、オプション・アクセサリー等(ソーター、DF、複写機専用台類)を考慮しない製品本体を対象とした。また、全ての部品は国内で調達し、使用、廃棄・リサイクルも国内で実施すると仮定した。環境負荷は、主にCO2排出量を考慮し、積み上げ方式を基本として算出した(一部、産業連関方式を利用)。
複写機のCO2排出量割合を算出した結果を図1に示す [4]。複写機の使用時における負荷が大きく、特にPPC用紙、電力、メンテナンスなどが大きな影響を与えることがわかった。
 |
| 図1 複写機のCO2排出量割合(改訂前) |
1.4.3 感度分析
図1の結果に対して、次の2つの分野で感度分析を利用した。
1) 結果に大きな影響をあたえるデータ要素を抽出するツールとしての利用(LCAの再調査への利用)
2) 環境負荷を低減させるために、どこに着目したら良いかを見つけ出す改善分析のツールとしての利用。
それぞれについて、以下に具体的に述べる。
(1)感度分析を利用した複写機LCAの再調査
上記、日本事務機械工業会における複写機LCAの実施目的は、主に算出モデルの構築であったため、データの正確さはそれほど重要と考えなかった。しかし、産業連関方式で詳細に検討した結果[2]と大きく異なる部分があったため、積み上げ方式による再調査を実施した。
複写機のLCAを算出するためには、約220個のデータ要素を必要としたが、これらのデータをすべて再調査することは非常に労力が大きい。しかし、LCAの計算に用いる全てのデータの不確実さが結果に大きく影響するわけではない。結果に対する感度の大きなデータを優先的に再調査することで、再調査に必要な労力を大幅に削減することが可能と考えた。
| 表1 複写一枚当たりの感度(改訂前) |
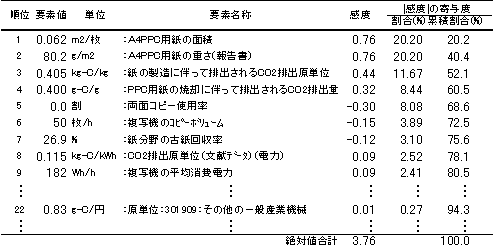 |
「複写一枚あたりのCO2排出量」に対する各データの「感度」を算出した結果を表1に示す。ここで、感度とは(CO2総排出量の変動率)を(データの変動率:10%)で割った値と定義する。例えば、「A4PPC用紙の面積」の感度は、0.062を1.1倍した時のCO2総排出量を再計算し、その値をもとのCO2総排出量で割った値から1を引き、さらに0.1で割った値(10倍した値)とする。
感度の絶対値の総合計に対する各データ要素の感度の割合を見ると、上位9要素で感度の総合計の約8割を占め、また上位22要素(総データ220要素の10%)で約9割を占めていることがわかった。注目すべきデータを絞ることの必要性が理解できるだろう。
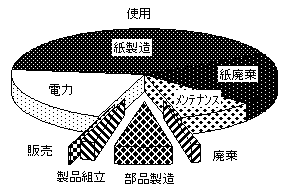 |
| 図2 複写機のCO2排出量割合(改訂後) |
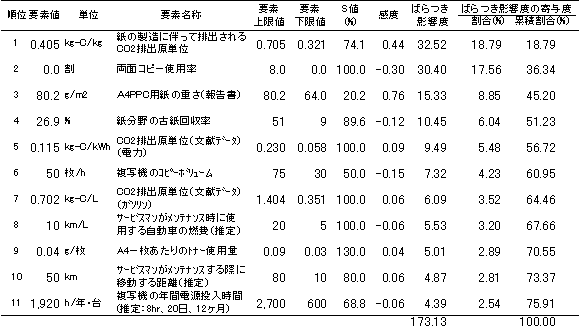
次に、複写機のLCAの再調査を行うために、感度を部分的に補正した。「A4PPC用紙の面積」は感度が最も高いが、この値はJIS規格があることから他のデータの曖昧さに比べて著しく小さいことが期待でき、感度が大きいにもかかわらずデータの曖昧さが結果に与える影響は小さいと考えられる。この影響を加味するために、「感度の絶対値」と「各要素値のばらつき」との積を「ばらつき影響度」と定義して、この値が大きな要素値から再調査を実施した。尚、「各要素のばらつき」を正確に求めることは難しいため、各要素の(上限値−要素値)と(要素値−下限値)のどちらか大きい方を要素値で割った値(S値)を便宜的に用いた。ばらつき影響度の算出結果を表2に示す。また表2を用いて複写機LCAを見直した結果を図2に示す。
| 表2 複写一枚当たりのばらつき影響度(改訂前) |
 |
(2) 複写機の改善分析への応用
製品の改善点を抽出する観点から見ると、感度が大きいデータ要素は環境負荷削減に大きく寄与する要素であることがわかる。これを利用して製品設計においてどこに注目すべきかの優先項目を抽出することができる。表3はLCAデータの再調査した後の感度分析結果だが、「複写機の平均消費電力」や「両面コピー使用率」の感度が高いことは、複写機の使用時の消費電力を削減することや両面コピー使用率を向上させること等が環境負荷削減に効果があることを示唆している。
| 表3 複写一枚あたりの感度(改訂後) |
 |
さらに、感度の値から製品設計の具体的な指針を得ることもできる。表3の「複写機の平均消費電力」と「複写機の部品購入費用総額」の感度は、それぞれ0.21、0.07となった。これは、複写機の消費電力を1割削減することと、そのために部品購入費用総額が3割増加することが同じ事を意味している。つまり、消費電力を1割削減するためにより高価な部品を使わなくてはならない(すなわちより環境負荷が大きくなる)というジレンマに対して、コストアップが3割以下であればCO2排出の観点からOKだと理解できる。
(3) その他の感度分析の利用について
・ 複写機のような多くの部品から構成される組立機械のLCAを実施する場合は、様々な簡易化を試みることになるが、安易な簡易化は誤った結果を導きかねず、常に簡易化の効用とその限界を考慮する必要がある [5]。簡易化を試みる場合は予備的なLCA結果に対して感度分析を実施して、それらが影響を与えないことをチェックすることが重要と考えられる。
・ 「データの曖昧さが結果に与える影響の大きさ」をLCA結果の読み手に伝えるために、感度分析を利用することもできる。感度の大きなデータ要素を感度値と共に公開するとよいだろう。
・ ある公開されたLCAについて、使用されている主要な原単位(例えば単位電力量あたりのCO2排出量)を任意の値に変更したときのLCA結果を推定することができる。従来は、複数のLCA結果を比較/マージする際に、使用した原単位を任意の値に統一することがデータの機密の関係から難しかった。
1. 4.4 誤差分析
LCAを実際に用いる際の大きな課題の一つは、得られた結果がどの程度信頼おけるかの指標が明確でないことだろう。
一般的に、結果のばらつきは、算出方法が適切でないこと(信頼性・再現性・整合性があるかどうか)や用いているデータのばらつきが大きいこと(地理的・時間的なばらつきが考慮されているか、平均値なのか特定値なのか(代表性)、データを算出するための範囲が適切か(完全性)、同一ロットのデータのばらつき(精度)が適切か等)が原因で引き起こされると考えられる。誤差分析は、特にデータのばらつきに対して有用な対処法の一つとなると考えられる。
誤差分析の最も多い利用法は、複数のケースにおいて算出された環境負荷量の間に優位な差があるか否かを判定することだろう(製品間の比較やステージ間の比較など)。そのための最も簡単なやり方は、データや仮定を確かめたい結論が不利になる様に再設定した場合で再計算し、それでも結論が変わらないことを確かめる方法である。例えば、最も初期の複写機のLCA(データ数約80個)において、「部品・素材製造のステージ」≦「使用のステージ」であることを確かめるために、「部品・素材製造」に有利に、「使用」に不利にデータや仮定を設定し直し、なお結論が変わらないことを確かることが出来た[2]。この例は、非常に簡単な計算結果でも、曖昧さをコントロールすることで有益な結果が得られるよい例だと考えている。(原田[3]は上方推定値という概念を用いて素材・部品・製品・サービスの各種原単位データの曖昧さを表現し、予備的なLCAを実施する上での応用を提案している。上方推定値からデータの上限値を推定し、上記やり方に応用することも可能だろう。)
しかし、このやり方は、データ数が少ない場合はある程度有効な手法だが、データ数が増えてくると結論が得にくくなる。データ数が増えるほど、あるデータのばらつきと別のデータのばらつきが相殺されやすくなるが、その寄与が考慮されていないためだ。そこで、その効果を反映させるべく、下記に示すモンテカルロ手法を検討した。
(1) モンテカルロ手法を利用した誤差分析
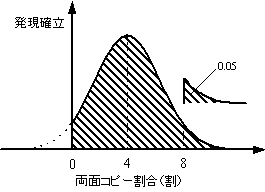 |
| 図3 両面コピー割合の分布(仮定) |
複写機のCO2排出総量について、その値の曖昧さをモンテカルロ法を利用して試算した。具体的には、約220個のデータ一つ一つについて、データの変動やその変動確率が一定の分布(密度関数)に従うと仮定し、その分布に従ってランダムにデータを変動させてCO2総排出量を再計算することを繰り返した。
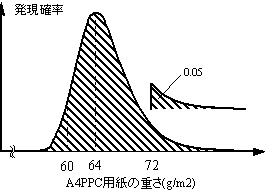 |
| 図4 PPC用紙重量の分布(仮定) |
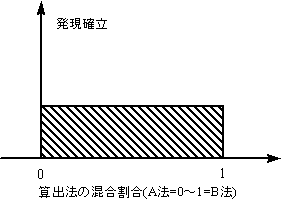 |
| 図5 算出法の混合割合分布(仮定) |
密度関数は、例えば複写機の両面コピー割合の場合、図3に示すように「4割」を中心とした正規分布と仮定した。正規分布の広がりは、(上限値−要素値)と(要素値−下限値)のどちらか大きい方の値以上の確率が5%と仮定して求めた(従って上限値以下かつ下限値以上の確率は90%以下)。ただし、「両面コピー割合」の場合は、0割以下の数値は取り得ないため、分布は図3にしめすハッチングの部分のみを考慮した。また、PPC用紙の重さの場合は、図4に示すように「64g/m2」を中心とした対数正規分布(実データの対数の値が正規分布に従うとする分布)と仮定した。分布の広がりは、対数軸上の正規分布について、上記と同様に(上限値−要素値)と(要素値−下限値)のどちらか大きい方の値以上の確率が5%と仮定して求めた。
密度関数は上記2つを基本型としたが、他にも上記分布の上限側、あるいは下限側をカットしたり、場合によっては図5に示すように一定の値の間を均等に分布する関数(複数の仮定で算出した結果を統合するパラメーターに適応)を想定した。
各データを上記密度関数に分布するようにランダムに変動させた時のCO2総排出量を約一万件収集して、そのヒストグラムを求めた(図6)。平均5.9g-c/枚、標準偏差1.6g-c/枚の対数正規分布に近い分布となることがわかった。これらの結果に対して統計解析の手法(母平均の差に関する検定や推定等)を応用すれば、同一製品のステージ間、あるいは2つの製品間の比較が数学的に処理可能となる。データの曖昧さの問題を確率の問題へと変換することで、意思決定にLCAを応用することがより容易になると考えられる。
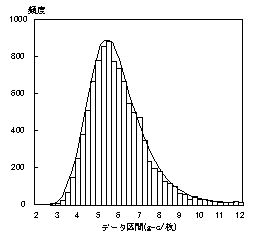 |
| 図6 CO2総排出量の算出結果 |
なお、上記モンテカルロ手法で用いた上限値と下限値は、多くを感度分析で用いた値から流用したが、感度分析で用いた以上にこれらの設定値が重要になっている点に注意を要する。それほど感度が大きくない要素に関する最大値と最小値は適当に大き目に設定した値を利用すればよいが、場合によっては、最大値と最小値を再設定する必要がある。感度分析と誤差分析は互いに影響しあっているため、実際の作業は両者を交互に利用しながら進める必要がある。
(2) インパクトアセスメントへの誤差分析の利用について
インパクトアセスメントに関する研究は、いまだ発展途上であるといわれている。例えば地球温暖化係数やオゾン層破壊係数は、ある程度科学的に決定することが可能であるのに対して、環境負荷項目間の重み付けやさらにはカテゴリー間の重み付けが純粋に科学的に決定することが難しいことがその理由とされる。しかし、それらの重み付けが一定の数値でなく、ある分布を持った密度関数で与えられるのであれば、インパクトアセスメントにも上記のような誤差分析を適用して各種目的に利用できると考えられる。各種研究から導かれた重み付け係数の最大値と最小値から密度関数を想定するなどの研究が進むことを期待したい。
1.4.5 終わりに
複写機LCAに感度分析と誤差分析を試みた事例を紹介した。この事例から、どのようなデータであっても少なからず曖昧さがあるが、その曖昧さを小さくすべく努力するよりも「データの曖昧さをコントロールしながら有用な情報を得る」努力が重要であることが理解できた。感度分析や誤差分析はそれを達成するために必要欠くべからざる存在であり、これら手法の確立なくしてLCAの実用化は望めないと考えている。
(キヤノン株式会社、LCA研究室 伊藤健司 執筆)
参考資料: