 |
|
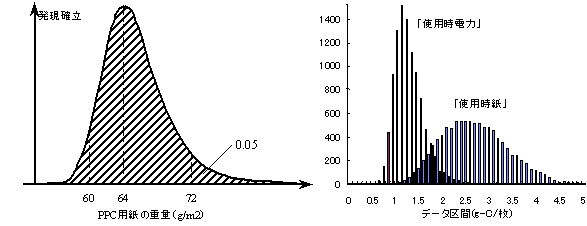
| 図1 PPC用紙重量の確率密度関数 | 図2 紙と電力のCO2排出量の分布 |
科学技術庁、平成11年度環境基本計画推進調査費LCA応用施策に関する検討調査「物質・材料の研究開発および選択におけるLCAの導入に関する調査」報告書、64〜71(2000)
2.7複写機のLCAにおける不確実性評価
2.7.1はじめに
日本事務機械工業会は、複写機のLCA事例を通して、LCAを意志決定に利用する場合のいくつかの課題解決を試みてきた。主な課題は、インベントリデータ収集の省力化手法開発に関すること。そして、「曖昧なデータ・仮定から有用な結論を得る」ことが果たして可能かどうかを見極めることである。
複写機の部品点数は通常数千〜数万点ある。そのため、単純に一点一点を積み上げ方式で調査することは不可能に近い。何らかの簡易化・省力化を導入すれば、結果の信頼性の欠如をいかに評価するかが重要になる。
日本事務機械工業会は、上記課題について不確実性評価手法を用いて検討し、いくつかの有益な結論を得るに至った。「感度分析」は、個々のデータ・仮定がLCAの結果に与える影響の大きさを分析する手法で、結果に大きな影響を与えるデータ・仮定を抽出することを通して省力化に利用できる。「誤差分析」は、LCA結果の比較評価の曖昧さを評価する手法で、データの曖昧さを加味した結論を得るために利用できる。
本報告では上記手法および検討結果のいくつかを紹介し、マテリアルセレクションのための「不確実性評価」手法について考察する。
なお検討した複写機は、1996年に国内販売された平均的なアナログ普通紙複写機(30枚/分)で、CO2排出量についての検討結果を示す。
2.7.2複写機における不確実性評価手法(1):感度分析
感度分析を使うためには次のような準備を必要とする。
複写機のLCAの場合、根拠のはっきりしたデータにまで極力さかのぼったデータ(源データ)は220個になった。これらのデータの一つ一つは、一定の誤差を持っている。例えば、「両面コピーの割合」は、ある調査によれば4割程度だとわかったものの、
などの観点から、0割(両面コピーしない場合)から8割(現場の直感からの最大値)まで振れる可能性があると考えた。これらの値は、データの曖昧さを比較的大きめに考えた時の可能性であって、実際はそこまでデータが振れる事はないだろうとの観点からそれぞれ上限値、下限値と呼んでいる。
感度分析を用いて「信頼性の高いデータを効率よく収集する」ためには、各データを一定の微少変動させたときの結果の変動の割合、すわなち
| 感度=(結果の変動割合)/(データの変動割合) |
ではなく、感度とデータのばらつきを組み合わせた、
| ばらつき影響度=(感度の絶対値)x(データのばらつき:S値) |
を用いる。ばらつき影響度が大きい順にデータを再調査して要素値、上限値、下限値を再設定することで、結果の全体としてのばらつき(各ばらつき影響度の絶対値の総合計と同義)を効果的に下げる事ができる。
感度分析を実際に利用するために、以下のようないくつかの工夫をした。
2.7.3複写機における不確実性評価手法(2):モンテカルロ法による誤差分析
モンテカルロ法とは、乱数あるいは物理的なランダム現象を利用した実験を通して、モデルがどのようなふるまいをするかを数学的に解析する手法である。本来は確率的な変動要因を含まない決定論的な問題に対して確率論的に解析する手法のことだったが、現在は、乱数を使ったモデル解析手法の総称として用いられる。
誤差分析は、LCAに用いたすべての源データについて、一定の確率密度関数にそってランダムに変動させた時の結果の集合を数学的に処理することで実施する(詳細は前報2)参照)。
例えば源データの一つである「PPC用紙重量」は、本来の調査値である64g/m2を中心とした対数正規分布型確率密度関数(図1)と置き換える。確率密度関数は、要素値64g/m2、上限値72g/m2、下限値60g/m2から計算ソフト(エクセルマクロ)を使って決定する。
| 「PPC用紙重量」:=64x1.125^(NORMSINV(RAND())/1.65) | |
| ただし、 | NORMSINV()は標準正規分布の%点を算出する関数、 RND()は0〜1の間の乱数を発生させる関数 |
同様に、すべての源データを乱数発生させる関数に置き換え、数千〜数万回乱数発生させることで、CO2排出量結果の集合を得る。
 |
|
| 図1 PPC用紙重量の確率密度関数 | 図2 紙と電力のCO2排出量の分布 |
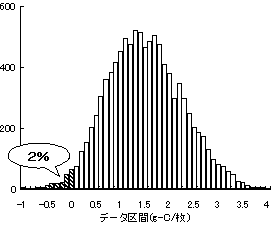 |
| 図3 (紙のCO2排出量)−(電力のCO2排出量)の分布 |
複数のLCAの結果を比較するために、結果の集合を数学的に処理する。例えば、ステージ間の比較として、「使用時の紙の消費と電力消費のどちらがライフサイクルのCO2排出に寄与しているか」を調べた結果を図2に示す。中心値でみると、紙消費が電力消費よりも約3倍CO2排出に寄与しているが、結果の集合をみると紙消費が電力消費よりも小さくなる可能性も幾分あることがわかる。紙と消費電力の両方に同じように寄与するデータもあるため、(紙の消費に伴うCO2排出量)−(電力消費に伴うCO2排出量)<0になる割合を調べると2%程度(図3参照)となった。データや仮定の曖昧さを考えても、「紙の消費の方が電力消費よりもCO2排出に寄与している(信頼率≒98%)」といえる。
モンテカルロ法を応用した誤差分析の利点を以下に示す。
2.7.4マテリアルセレクションへのLCAの応用
一般に、LCAを実施する際には以下のようないくつかの課題を解決する必要がある。
これらの課題はあまり問題にならないケースもある。例えば複写機の両面コピーを推進するように改良を加えるべくLCAを実施するような場合は、改善部位が少なくかつ紙の影響が著しく大きいため、多少のデータの欠如や信頼性のなさは比較的評価に影響しにくい1)2)。さらに、両面コピーを推進することですべての環境負荷が低減される傾向にあるため、インパクト評価も特に必要としない。
実用面から言って、LCAによく似た手法として環境影響評価や製品アセスメントがある。その評価基準や方法は、多くの場合定性的かつ主観的にならざるを得ないが、運用面ではあまり問題にならない。それは、現代社会が環境問題に真剣に取り組み始めてから日が浅く、評価の「あらさ」よりも、とにかく何らかの手を打つことによるメリットの方が十分に大きいためと考えられる。LCAによる評価は少なくとも上記評価手法よりも科学的であり、それらが担ってきた役割の幾分かをLCAで代用することによる社会的なメリットは十分に大きいと感じている。その視点からもう一度LCAのデータの曖昧さを見直すと、データが曖昧であっても十分に利用価値がある分野が存在することは直感的に理解できるだろう。
一方、「マテリアルセレクションへのLCAの応用」は、上記用途と異なり、完全とは言いにくいデータを用いて微妙なLCA結果を解釈する必要があり、多くの場合インパクト評価も必要とする。
それでもなおこの分野にLCAを適用しようとするならば、前述した「不確実性評価」手法は是非とも導入する必要があると考える。以下に、不確実性評価を導入することの重要性とその課題などについて考えを示す。
2.7.5インベントリデータ収集の省力化と不確実性評価
「LCAを意志決定のツールとして用いる場合は不確実性評価が重要」との話をすると、「不確実性を評価することよりも、信頼性の高いデータの収集あるいはデータベース構築が重要」との意見が多くだされる。また、比較的部品点数が少ない製品のLCAは、かなりの努力をすればなんとかデータを収集することができる見通しがあるためか、LCAの省力化について十分な関心が向けられていないように見受けられる。
実際は、「すべてのデータを高い信頼性を保って収集すること」はかなり努力しても難しく、部材の多寡にかかわらず適切な省力化とそれに伴う不確実性評価が重要と考える。言い方を変えれば、LCAに必要なすべてのデータをきっちりと集めることができないために、「不確実性評価」というツールを使って現存するデータだけでなんらかの結論を得ようとする必要がある。
省力化を進めつつ結果の信頼性を向上させるために必要と考えられる事柄を以下に示す。
2.7.6不確実性評価手法を実施するための工夫と手法としての信頼性
感度分析に使用したデータは、各データの上限値、下限値である。CO2排出量を算出するためのデータ数は220個あるため、単純に計算すれば、合計660個の要素値、上限値、下限値を調査・収集する必要がある。しかし、本事例では全部の上限値、下限値を最初から調査・収集しなかった。それは、結果に対してほとんど影響しないデータは、その上限値、下限値共に感度算出に対してほとんど影響しないと考えたためである。
結果に大きな影響を与えるデータは、ばらつき影響度の上位20位(全データ数の一割!)程度だったため、上限値、下限値もそれらについてのみ精査した。それ以下のデータについては、要素値と同時に上限値、下限値を得ることができたデータ以外は、要素値の定数倍(例えば3倍)を上限値、定数の逆数倍(例えば1/3倍)を下限値として設定した。その影響については下記誤差分析と併せて考察する。
モンテカルロ法を応用した誤差分析は、
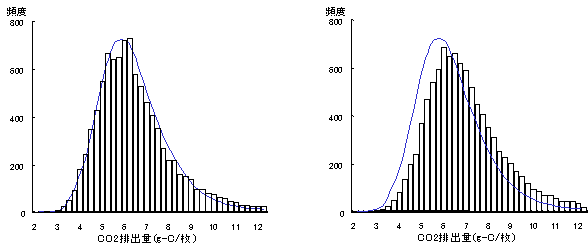
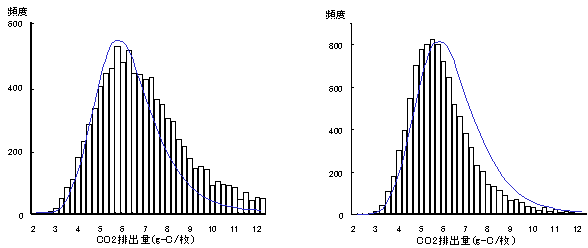
をそれぞれ決める必要がある。図4に不明定数2倍、関数形状が正規分布型、確率割合10%の複写機CO2排出量の分布を示す。図4の各種条件のうち不明定数のみを3倍に変更した場合を図5に、同確率割合を20%に変更した場合を図6に、同関数形状を対数正規分布に変更した場合を図7に示す。図4〜7に示す実曲線は、図4の分布のスムージング曲線を示した。
 |
|
| 図4 標準のLCA結果 | 図5 不明定数を3倍にした場合 |
図4〜7を比較するとCO2排出結果の分布は、それほど大きく変化が無いことがわかる。さらに、関数形状に関しては、上限値、下限値の間を均等に分布する均等分布関数を用いても同様に結果にあまり影響ないことを確かめている。
ばらつき影響度の小さいデータの上限値、下限値を不明定数を用いて処理することと、モンテカルロ法に必要ないくつかの係数が結果にあまり影響しないことから、感度分析および誤差分析は手法としての利便性・信頼性が高いことが示唆される。特に、感度分析が実施済みであれば、モンテカルロ法を利用した誤差分析を追加実施するために必要な労力はほとんど必要としないことは特筆に値する。
 |
|
| 図6 確率割合を20%にした場合 | 図7 対数正規分布に変更した場合 |
2.7.7インパクト分析への不確実性評価手法の応用
上記不確定性分析はインパクト分析の特性係数等の曖昧さにも適用できると考える。例えば、IPCC(1995年)が示す地球温暖化の係数は、CO2に対してCH4が56〜6.5倍、N2Oが310〜170倍としている。地球温暖化の積算年数をいかに考えるかによって効果が異なることに起因する(20〜500年)。この場合は、例えば表1に示すように要素値を決めてインベントリデータの曖昧さと同様にインパクト分析の感度分析、誤差分析が可能である。
| 表1 地球温暖化係数への適応例 | |||||||||||||||
|
BOD、COD、T-P、T-Nのような環境負荷は、排出によって水圏の濃度が一定値以上になる場合にのみ環境負荷として認識される。この場合は、最悪/最善の状態を仮定して感度分析を行い、また閾値を決定する関数および閾値以上の影響を示す関数が求められれば、それぞれの関数で用いる係数の上限、下限を表1と同様に設定することで、誤差分析を行うことが可能となる。
インパクト分析における地域依存性、時間依存性、さらには最終的な重み付け係数なども同様の処理が可能であると考える。不確実性分析を前提にした基本データの収集などが望まれる。
2.7.8不確実性評価手法の課題
感度分析は、分析手法にいくつかの考え方があるものの、実用性の観点からはほぼ確立されたと考えて良いだろう。いくつかの技術的な部分について、つめの議論が活性化することが望まれる。
モンテカルロ法による誤差分析は、実施例があまり見あたらず、また活発に議論されている分野ではない。モンテカルロ法を利用した誤差分析の課題を以下に示す。
2.7.9終わりに
LCAを意志決定に利用する場合は、インベントリの省力化やインベントリ/インパクトの曖昧さの極小化は重要な課題となる。しかし、不適切な省力化は曖昧さを増大させ、逆にすべてのデータ・仮定の曖昧さをゼロに近づけようとすれば膨大な算出時間が必要となる。要は、「曖昧さをコントロールしつつ早くかつ有用な情報を得ること」が重要であり、その意味において、不確定性の評価は、LCAを意志決定に利用するための中核の技術であると考える。マテリアルセレクションなどの「LCAの意志決定への応用」のためには、不確実性評価手法のさらなる検討が望まれる。
(科学技術振興事業団 伊藤健司 執筆)
参考資料:
1) LCA実務入門編集委員会編、「LCA実務入門」、産業環境管理協会(1998)
2) 伊藤健司、日本事務機械工業会における感度分析、誤差分析の取り組みについて、平成10年度環境基本計画推進調査費LCA応用施策に関する検討調査「物質・材料の研究開発および選択におけるLCAの導入に関する調査」報告書、科学技術庁(1999)、19〜25