今回は、LCA(ライフサイクルアセスメント：環境負荷を把握する手法→前々回参照）と手法的にはほとんど同じLCCをつかって、「データの曖昧さ」をマネージメントする手法について取り扱います。今回も、例の4人がT先生をお呼びしているようです。
| egg | 今回は、前回に引き続き、洗濯機のライフサイクルコスト、略してLCCについてＴ先生に講義を受けたいと思います。 それではさっそくですが、･･･ 前回のLCCの計算で、疑問に思うことがいくつかあります。 例えば、計算に使っていた洗濯量が私の家庭よりもかなり少ないように感じるのですが･･･ |
|||||
| T先生 | 前回お話したように、この計算は私の家庭の実情を反映しておる。したがって、一日あたり3kgの洗濯量というのはたしかに一般家庭よりも少ないかもしれん。しかし、前回も申し上げたように、計算の目的が3年前に「私が洗濯機を買うとしたら、なにをセンタク（選択）するか」だからネ･･･ | |||||
| egg | ダジャレはともかくとして、･･･ 私の家庭に当てはめるとどうなのかが知りたいんです。 |
|||||
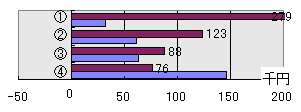
| T先生 | そういった要望は当然出てくるじゃろうな。そこで今後数回は、前回の洗濯機のLCC計算をエッグちゃんの家庭にとどまらず、もっと一般的な家庭に当てはめるとしたら、どこをいじらなければならないかについて取り扱うことにしよう。 下の図１に、前回の結果と同じグラフを示す。 今後は、この中から特に特徴的な4つの製品①～④について取り扱うことにしよう。この4つの製品のLCCを考える上で、重要なポイントが3つある。今回はそのうちの最初のポイントになる「感度分析手法」について取り扱うことにしよう。ちょっと、難しく思うかもしれんが、これはLCCだけではなく、LCAやその他のシミュレーションを実施する上で「核」となる技術じゃ。直感的に理解できるだけでもかなり役に立つと思う。かんばってついてきてくれたまえ。 では、まず最初に、エッグちゃんが関心のある洗濯量の違いから検討してみよう。 |
|||||
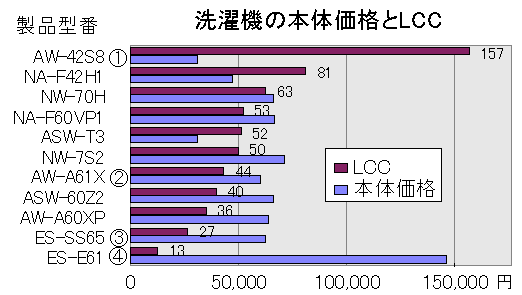 図１ 洗濯機の本体価格とライフサイクルコスト（標準結果) |
||||||
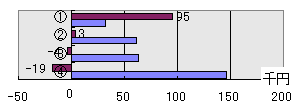
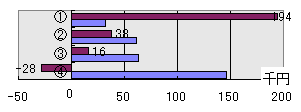
| 図１の計算の時には、洗濯量が年間1.4ｔとしたんじゃが、それを倍の2.8tにして再計算したものを左下図の図２に示す。同じように、洗濯量を半分にした0.7tのものを右下図の図３に示す。 ちなみに、図３の中のの「-19」とは、この④の洗濯機を使うことでクリーニングなどをしなくて良くなることから、費用よりも利益が増えて、「④の洗濯機を買うことで、洗濯機を使わないよりも差し引き1.9万円のお得」になるということじゃ。 そういえば、前回の「洗濯機のLCC（その１)」に対して読者からコメントがあった。 『LCCの内訳にマイナスの費用が表示されるのは、いかにも分かりにくいと思います。むしろ、クリーニングに出すワイシャツ枚数を含めた洗濯総数を機能単位として、ＡＷ－４２Ｓ８①などはクリーニング費用を足すべきだと思いますが・・・・。』（Y氏） ということじゃった。つまり、「洗濯機のLCC」ではなく、「洗濯機と衣類のLCC」とした方がわかりやすいというご意見じゃ。確かに研究者に対してではなく市民に対して話をするのであれば、その方がわかりやすいかもしれん。じゃが、「洗濯機と衣類のLCC」とすると、作業が少し増えることになる。また、作業が増えるだけ結果の曖昧さが増えることになる。ということで、わかりやすさよりも、作業性・信頼性を優先したんじゃ。このあたりは、実際にこれを読まれている読者からご批判・ご意見をいただけたらと思う。 ということで、今までのやり方でとりあえず進めることにする。 |
||||||
|
||||||
| 豆腐 | 図２、図３のグラフは面白いですね。カーソルをグラフの上に持っていくと、元の年間1.4tのグラフが出てくるんですね。 えっと･･･ この図を見ると、洗濯量が元の値の倍、あるいは半分になる程度では、「④の洗濯機のLCCが最も小さい」との結論は揺るがないことがわかりますね。 |
|||||
| T先生 | このように、特定の条件下では、データが比較的曖昧でも結論がひっくり返ることがない性質があり、これを「倍/半分の法則」というじゃ。 | |||||
| 人参 | そんな法則があるなんて初耳ですね。それは本当のことですか？ | |||||
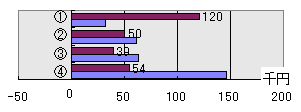
| T先生 | 「うそ」じゃ。そんな法則はない。じゃが、そういった性質があるのは事実じゃ。詳しくは次回以降述べることにして・・・ 次に行ってみよう。次は洗濯機寿命じゃ。もともと10年としていたが、これを13年にしてもう一度計算したものを左下の図４に示す。逆に7年にしたものを右下の図５にそれぞれ示す。 |
|||||
|
||||||
| 豆腐 | 寿命が13年の時は良いんですが、寿命が7年になったら「④が最もLCCが小さい」との結論が成り立たないことがわかりますね。 | |||||
| Ｔ先生 | そうじゃな。多くの家電製品の平均寿命は10年程度であることがわかっているが、短くなるほど本体価格が効いてくるんじゃな。「寿命が10年以下の場合は結論はなりたたない」可能性があることに注意する必要があることがわかった。 次に行ってみよう･･･ |
|||||
| egg | この調子で全部のデータを調べるのは大変じゃないですか？例えば、寿命が長くなった場合は調べなくても、短くなった場合だけ調べれば良いんじゃないですか？ | |||||
| T先生 | なかなか良いことをいってくれるな。「④の洗濯機のLCCが最も小さい」との結論に不利になるようにデータをセットして再計算すればよいから、多くの場合、「多くするか、少なくするか」どちらか一方だけ調べればいいんじゃ。このような性質を「線形性が成り立つ」状態というんじゃ。 | |||||
| egg | 「センケイセイ･･･」？ 今度は本当なんでしょうね！ |
|||||
| T先生 | ほほほ･･･ 今度は本当じゃ。ほとんどの計算ではこれが問題なることはないが、複雑な計算や、「倍/半分」よりもデータの曖昧さが大きい場合などは、問題になることがある。このことも次回以降取り扱おう。 元に戻って･･･ 左下の図６は洗剤費用を「④の洗濯機のLCCが最も小さい」との結論に不利になるように、2倍の20円にした場合を示す。 右下の図７は衣服寿命延命割合が同じく結論に不利になるように、半分の0.1にした場合を示す。 |
|||||
|
||||||
| egg | 衣服寿命延命割合というのは、④の洗濯機が衣服をやさしく洗い上げるので、結果として新しい下着類を買わなくてもすむ割合でしたよね。要するに「衣類へのやさしさ指数」が半分になった場合ですね。 洗剤は結論には影響していないけれど、この衣服寿命延命割合を半分の0.1にした時には結論を否定する結果になるんですね。 |
|||||
| 豆腐 | いずれにしても全部のデータをこうやって調べるのは結構大変ですね。 | |||||
| T先生 | そうじゃ。こういった、定型の作業は、コンピュータに任せればよいんじゃ。 そこで、「感度」といったものをきっちりと決めて、ボタン一つでコンピュータに計算させることにしよう。「感度」は、読んで字の如し。感じる度合いじゃ。 データを「ちょこっと」いじってやると、結果が驚くほど変化するのか、それとも変化しないのかを数字で表現したもので、次の式で定義する。 「感度」＝（結果の変化率）÷（データの変化率） |
|||||
| egg | 数式嫌い･･･ | |||||
| T先生 | いや、具体的にやれば全然難しくない。例として、上の洗剤費用の場合について順番に計算してみよう。
|
|||||
表１ ③のLCCから④のLCCを引いた値に対する感度分析結果 |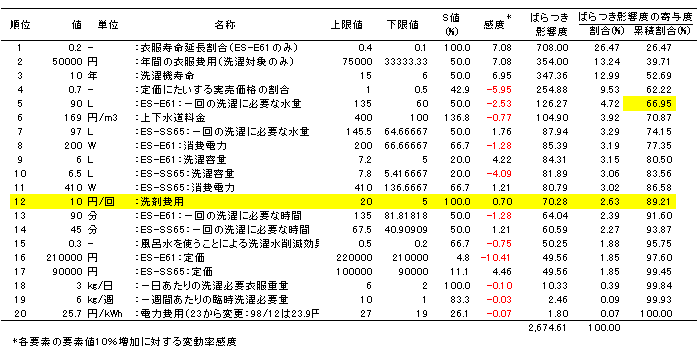
||||||
| 豆腐 | 感度の値がマイナスになっているものがありますが、どういう意味ですか？ | |||||
| Ｔ先生 | データを増加させた時に結果が増加すればプラス。データを増加させた時に結果が減少すればマイナスになる。例えば、4番目の「定価に対する実売価格の割合」を見てみる。 元々は「定価の7掛け」と考えたんじゃが、この「0.7」を1％増加させると、「③のLCCから④のLCCを引いた値」は5.95％減少するんじゃ。今回のような用途に使う場合は、プラスマイナスは無視して絶対値の大きさだけを見ればよい。 |
|||||
| 豆腐 | 「ばらつき影響度」とはなんですか？ | |||||
| Ｔ先生 | そうじゃ。それを説明するのを忘れていた！ 実は、データのばらつきが結果に与える影響を見るときには、感度よりも「ばらつき影響度」を見るほうが望ましいんじゃ。 「ばらつき影響度」＝「感度」ｘ「S値」、ただし「S値」＝max（上限値-データ値、データ値-下限値） と定義するんじゃ。上限値とデータ値との差あるいは、データ値と下限値との差のどちらか大きい方をS値としてそれと感度を掛け合わせたものが「ばらつき影響度」じゃ。 F(x)の物理誤差＝Σ（∂F(x)/∂x）dx の（∂F(x)/∂x）が感度に相当し、dxがS値に相当すると言えば分かりやすい |
|||||
| egg | 「シグマ ラウンド えふえっくす??」･･･ ぜんぜん分かりません！！ | |||||
| Ｔ先生 | う～む。それでは･･･ 16番目の「ES-E61：定価」を見てもらいたい。感度の絶対値が最も大きい「10.41」になっているが、良く考えてみると、定価というものに、ばらつきはあるだろうか？アクセサリーなどが発生する可能性があったので、上限値を22万円とちょっと大きめに考えてはいるが、定価そのものは21万円でそれ以上でもそれ以下でもないだろう。 つまり、「④の定価の結果に対する感度は大きい」かもしれないが、「④の定価のばらつきは結果にあまり影響しない」といったデータが存在することもあるんじゃ。 感度だけでは、そういったことを加味するのが難しいので、個々のデータのばらつきを加味するために「ばらつき影響度」を導入したんじゃ。 まあ、計算はパソコンがしてくれるので、なんとなくわかる程度でよろしい。 |
|||||
| 豆腐 | それで、表１は「ばらつき影響度」の大きい順に並べてあるんですね。 ばらつき影響度の全体に対する割合を足し合わせると、5番目で「66.95」になります。すなわち5個のデータのばらつきが結果に対して2/3の影響をもつということになりますね。 それ以外のデータはあまり結果に対して影響をもたないんですね。 |
|||||
| Ｔ先生 | その通りじゃ。 実は、･･･ 表１の６番目の上下水道の値は問題がある。上下水道は、我々市民が支払っているお金だけでは運営されていない。補助金が同額程度つぎ込まれておる。LCCは、前回申した通り、自分のところだけではなく全ての工程における費用を考慮する必要があるから、我々市民が支払う169円/m3では、見落としがあると言わねばなるまい。 それに、･･･ 20番目の電力原単位も問題がある。需要家によって費用が異なるんじゃ。一般家庭なら25円程度じゃが、工場ならば16円、さらに大口ならばもっと安い単価になっておる。洗濯機のLCCを一般化しようとしたら、どの単価を使うのかが問題になるんじゃ。 しかし･･･ 表１に示すように、上下水や電力の費用は、結果にはあまり影響していないことが分かったんじゃ。これは、「当初設定したまま」で十分な結論が得られることを意味しており、故にあえて数字を見直すことをしなかったんじゃ。 このように、感度分析を実施することで結果が大きく変わるデータがどれかを見極め、それらを中心にデータの精度を高めるように工夫することで、効率的にLCCの計算ができるんじゃ。LCCやLCAなどのシミュレーションをやる時に、解釈が難しいデータがよく出てくるもんじゃ。しかし、それが結果にあまり影響しないのであれば、「適当」に処理できるんじゃな。 |
|||||
| egg | 計算を怠けるために感度分析をするんですか？ | |||||
| T先生 | それは誤解じゃ。 今回のLCCは単純な計算じゃったから、一日もあれば計算できた。しかし、ちょっと複雑なLCC、あるいは一般的なLCAは、一つ一つのデータをちゃんと調べようとすれば、それこそ数ヶ月、あるいは数年もかかってしまうほど大変なものになる。それだけ時間が必要になれば、実施費用も馬鹿にならない。ましてや商品寿命が数ヶ月しかないパソコンのようなハイテク製品に利用する場合などは、こういった計算そのものが意味を持たなくなってしまう。 お遊びでLCCやLCAをやるのであれば、いくらでも時間がつかえる。しかし、実際の意思決定にこれらの手法を利用しようとするならば、費やす時間を極力小さくする必要がある。まさに時間との勝負なんじゃ。 じゃから、上に示したような感度分析を実施することで実施時間を画期的に短縮する必要があるんじゃ。とっつき難いかもしれんが、計算そのものはパソコンがやってくれるので、「急がば回れ」的な効用があるんじゃな。 実際、LCCやLCAを実施すると、データの見直しを頻繁に行う必要がある。場合によっては、「全面やり直し」が必要になることも珍しくない。そんな時、一発で感度分析を実施してくれるプログラムがあれば、修正するたびに実施して、次にどこを注目すればよいかの指針が得られるんじゃ。感度分析は海を航海するときの羅針盤みたいな役割を果たすんじゃな。 じゃが、残念なことに研究者でもこのことをちゃんと理解している人があまりいない。そんなに難しいことは言っておらんのにどうして理解できんのか、それこそ理解できん。海に出るのに羅針盤も持たずにどうやって航海するんじゃ。まさに「コウカイ（後悔）」するぞ･･･ |
|||||
| egg | またくだらないダジャレを言ってますね。 ところで、単純な質問をしていいですか？ いくら感度が低いデータであっても、いくつかのデータをいいかげんに設定すると、相乗効果みたいなものが出て、結果が否定されるようなことになるんじゃないですか？ |
|||||
| Ｔ先生 | おお、それこそ次回のメインテーマである。まだ、手法としては名前がついておらんのじゃが、とりあえず「誤差分析」と名づける手法について、次回検討したいと思う。 「感度分析」の用途は、今回勉強した以外にもたくさんある。それに、「感度分析」は、LCCやLCAなどに限った話ではない。同様のシミュレーションを実施する場合は、知っていると知らないとでは雲泥の差がでる基礎的な技能でもある。よって、今回計算に使用したエクセルシートを皆さんに配布するので、良く復習してもらいたいと思う。あっちこっちの数字をいじって、感覚を養うだけでも役に立つと思う。ファイルの「data_base」シートに「感度分析」マクロボタンを配置してある。ちょっと走らせて遊んでみるのも面白かろう。 では、今日はここまでにしておこう。 |
|||||
T先生から配布されたエクセルシートを下からダウンロードできます。マクロをお使いになりたいときには、エクセルを立ち上げたときに「マクロを有効にする」ボタンをOKにしてください。
|
